
De acordo com Plotino (filósofo grego do século III dC), o “UM” é a realidade e a Fonte última de toda existência (Yael, 2006). Filo de Alexandria (filósofo judeu-egípcio nascido durante o século I aC) considerou o número “UM” como o número de Deus e a base para todos os números (“De Allegoriis Legum“, ii.12 [i.66]). Como todas as verdades, a natureza fundamental do “UM” é recorrente no tempo. Um exemplo é a evolução do signo escrito 1. Como a imagem abaixo mostra, começou com uma linha horizontal usada pelos indianos, e transformou-se e evoluiu até que surgiu novamente como uma linha, desta vez vertical. A busca pelo significado do “UM” está em curso ainda nos dias de hoje. Por exemplo, no início do século passado, o matemático e génio místico Ramanujan acreditava que todas as unidades emergiam do produto entre o zero e o infinito (Saymal e Ravi, 2016). E, no que a isso diz respeito, quem somos nós para questionar o homem que conheceu o infinito.
O início
Quanto mais se pergunta sobre algo, mais se tende a questionar os fundamentos do conhecimento. As nossas limitações são, antes de mais, as nossas fundações. Como é que os antigos definiam o Um? Como é que uma criança adquire o conceito de Unidade? Estas perguntas não são diferentes. O conceito de Unidade ou do “UM” emerge da repetição. Sem um padrão recorrente, não poderá haver Unidade. Se o Universo nunca foi repetitivo então os padrões nunca teriam existido nem a nossa capacidade de categorizar e analisar o nosso ambiente. Existe uma engrenagem Universal subjacente que impulsiona toda a Criação. Na realidade uma entidade emerge quando o nosso cérebro reconhece tanto a existência de um padrão como o seu desaparecimento. Por exemplo, o padrão de uma maçã repete-se na próxima maçã. Por outro lado, ele desaparece no espaço em torno da maçã. Ou seja, a nossa mente cria uma borda invisível que delimita um interior (o padrão, a maçã, que tipicamente é vermelha ou verde com uma forma arrendondada e com um pequeno ramo a sair do topo) de um exterior (o NÃO “padrão”, o não “maçã que é, por exemplo, a árvore, ou o chão onde a maçã caiu). Esta noção de separação entre o que “É” deu origem ao número 1, e a interação de diferentes “UNS” deu origem à geometria e à matemática.
A Vida de Fermat
Fermat era um filósofo e um matemático do século XVII. O seu interesse não era o de publicar artigos visto que na realidade ele não publicou nenhum. Foi o seu filho que tornou o seu trabalho conhecido depois dele falecer. O seu interesse era o de descobrir o desconhecido. E nisso ele foi bastante bem-sucedido. O seu famoso Teorema Último foi descoberto pela primeira vez na margem de uma cópia sua de uma edição de Diophantus, e incluía a afirmação de que a margem era muito pequena para incluir a prova (Singh, 2002). Não foi encontrado nenhum escrito dessa prova. A aparente simplicidade da prova (como sugerido pela declaração de Fermat) eludiu os matemáticos ao longo de séculos, incluindo grandes nomes da matemática como Gauss. O seu interesse exclusivo pelos números inteiros faz-nos questionar a sua profundidade na busca de respostas. Ele terá aprofundado o suficiente para questionar o significado de um número inteiro? Terá ele procurado o seu significado somente com a matemática ou expandiu-se para a geometria? Terá a perspectiva matemático-geométrica do significado de um número inteiro fornecido-lhe as ferramentas para resolver o seu (Fermat) último teorema?

A resposta a todas as coisas é o início e, afinal, uma árvore inteira sempre começa com uma minúscula semente de conhecimento. Um exemplo disto é a árvore ternária dos triplos pitagóricos primitivos que o Dr. Teia mostrou ser uma árvore nascida do triplo (3,4,5) e crescendo sempre com o mesmo movimento fundamental (Teia, 2016). Em última análise as perguntas “O que é uma unidade?”, “O que é um número inteiro?” “e qual é o significado do último teorema de Fermat?” Estão, de facto, profundamente inter-relacionados, de modo que a resposta combinada a todas as três é a solução para o Último Teorema de Fermat.
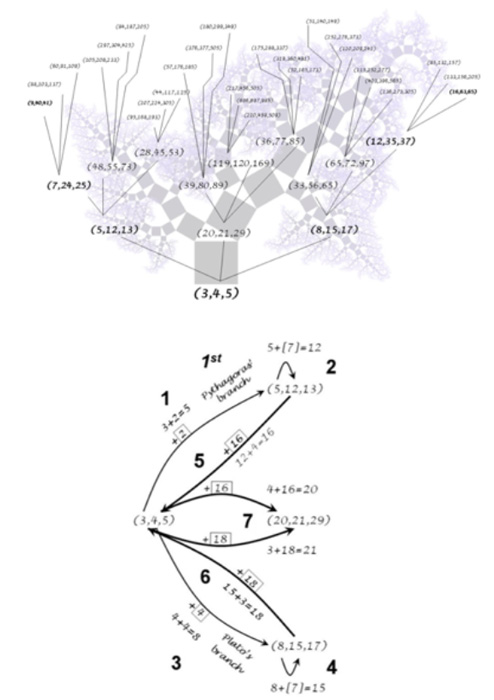
O Último Teorema de Fermat (Prova Geométrica)
No ano passado (2016), no artigo Origens Antigas intitulado “O antigo uso babilônico do Teorema de Pitágoras e as Suas Três Dimensões”, o Dr. Luis Teia apresentou a prova do teorema de Pitágoras em 3D. Este ano, o Dr. Teia explica no seu recente artigo publicado em Fevereiro de 2017, intitulado Teorema de Fermat – uma Visão Geométrica publicada no Journal of Mathematics Research, como essa compreensão 3D do Teorema de Pitágoras forneceu a base geométrica para provar o Último Teorema.
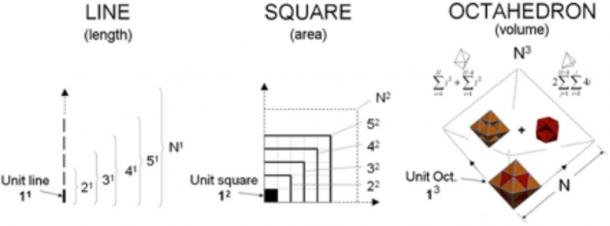
O Último Teorema de Fermat, também conhecido como conjectura de Fermat, é mais do que apenas sobre triplos, é sobre a natureza fundamental do número inteiro, e o seu significado matemático e geométrico. Ele levanta a questão filosófica: O que é uma Unidade? Na linguagem da matemática, uma unidade é definida pelo número 1. Na linguagem da geometria, uma unidade é definida por um elemento de comprimento lateral igual a 1. A perspectiva dum problema depende da linguagem que usamos para o observar, e uma mudança de perspectiva é muitas vezes tudo o que é preciso para ver a solução. Fundamentalmente, a prova de Teias afirma (como mostra a figura abaixo) que não existem inteiros geométricos (nenhum octaedro divisível unitário, que é o fundamento do teorema de Pitágoras em 3D) no reino do teorema tridimensional de Pitágoras, nem em Todas as dimensões mais elevadas.
Conclusão
A fundação – o significado do “UM” – está a evoluir. Como será daqui a 1.000 anos? A nossa expressão completa o ciclo e voltará a ser uma linha horizontal? A nossa compreensão matemática da realidade tornar-se-á mais uma vez complementada pela geometria euclidiana? Será que a nossa noção do que é um número inteiro e de como ele afeta qualquer teorema (incluindo o Teorema de Fermat) evoluiu paralelamente? A descoberta de Teia contribui para responder a essas perguntas (sobre o significado do “UM”, do que é um número Inteiro e o Último Teorema de Fermat). Não há verdade senão a verdade que encontramos para nós mesmos, e isso inclui a verdade de cada indivíduo e a busca pelo que é o “UM”. Quanto ao Dr. Luis Teia, o seu próximo desafio será o de explicar o significado geométrico do trabalho sobre partições do matemático Srinivasa Ramanujan.
Por Luis Teia
Fonte: http://www.ancient-origins.net/history/god-s-number-origins-one-007578?nopaging=1
English
Isenção de responsabilidade: Nós, do Prepararem-se para a Mudança, disponibilizamos informações que não são divulgadas pelos principais meios de comunicação e, portanto, podem parecer controversas. As opiniões, visões, declarações e / ou informações que divulgamos não são necessariamente promovidas, avalizadas, adoptadas ou em concordância com o Prepararem-se para a Mudança, com o seu Conselho de Liderança, com os seus membros, com aqueles que trabalham com o Preparem-se para a Mudança ou com os que leem o seu conteúdo. Contudo os artigos são, esperançosamente, provocadores. Por favor use o seu discernimento! Use o seu pensamento crítico, a sua própria intuição e a sua própria conexão com a Fonte, com o Espírito e as Leis Naturais para o ajudar a determinar o que é verdade e o que não é. Ao partilhar informações e semear o debate de ideias, é o nosso objectivo elevar a Consciência e o conhecimento das verdades mais elevadas, para libertar-nos da escravidão da matriz de controlo neste reino material.
 PT
PT EN
EN ES
ES FR
FR NL
NL DE
DE RU
RU SL
SL SV
SV TR
TR



















